Funzioni biunivoche

Una funzione è una relazione tra un insieme di partenza, $A$ , e un insieme di arrivo $B$ che associa uno e un solo elemento di $B$ ad ogni elemento di $A$ . Se la funzione è sia iniettiva che suriettiva si dice che la funzione è biunivoca.

Definizione

Definizione

Funzione Biunivoca

Data una funzione:

f: A \rightarrow B

Se la funzione è sia iniettiva che suriettiva si dice che essa è una funzione biunivoca o biiettiva. Inoltre, una funzione biunivoca si chiama anche corrispondenza biunivoca tra $A$ e $B$ .

In termini matematici devono valere entrambe le seguenti scritture:

\forall a \in A \quad \exists ! b \in B: f(a) = b

\forall b \in B \quad \exists ! a \in A: f(a) = b

In sostanza, una funzione biunivoca crea una relazione "uno ad uno" tra gli elementi del dominio e del codominio, per cui ad ogni elemento di $A$ corrisponderà uno e un solo elemento di $B$ e viceversa.

Graficamente questo concetto può essere espresso nella figura seguente:

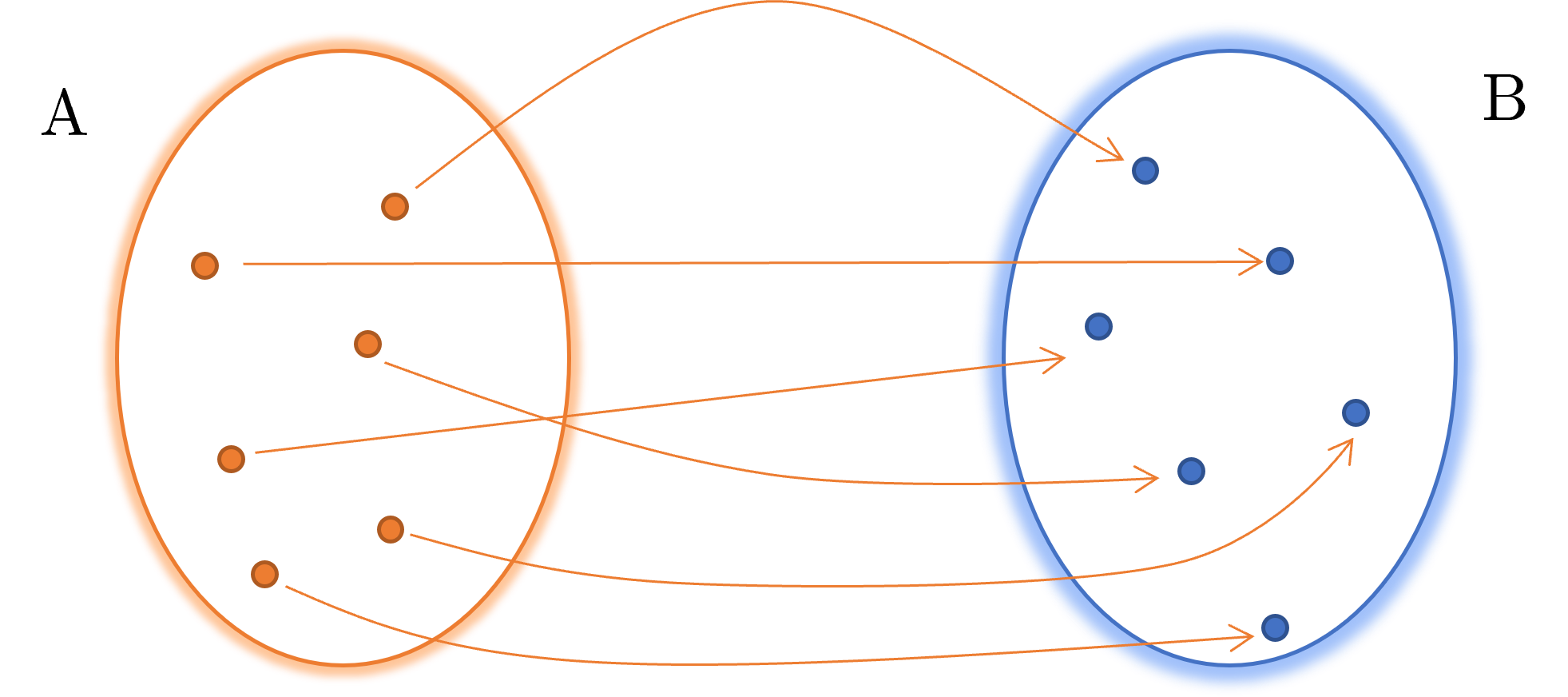
In sintesi

In questa lezione abbiamo visto il concetto di funzioni biunivoche, una categoria di funzioni per le quali esiste una relazione "uno ad uno" tra gli elementi del dominio e quelli del codominio.

Nella prossima lezione vedremo come, a partire dal concetto di funzioni biunivoche, è possibile ricavare il concetto di funzioni inverse.

Lezione Precedente Indice del capitolo